11. Местоположение ячейки, к которой должна передаваться информация от очаговой ячейки, определяется внутри СПИ как случайное.
12. Диффузия может прекратиться на любой стадии; однако, когда все ячейки в границах изучаемой территории получили информацию, никаких изменений в ситуации произойти не может и процесс диффузии на этом завершается.
Ключ к использованию модели содержится в правилах 10 и 11. В каждый интервал времени СПИ помещается над каждой очаговой ячейкой так, что центральная ячейка решетки совмещается с ячейкой-очагом. Затем берется любое случайное число из последовательности чисел от 0000 до 9999 и используется для нахождения адресата сообщения в соответствии с правилами 4—6. Случайные числа представляют собой набор чисел, выбранных абсолютно наугад. Их можно взять из публикаций таблиц случайных чисел или использовать программу для ЭВМ. Эта процедура отражена на рис. 20.
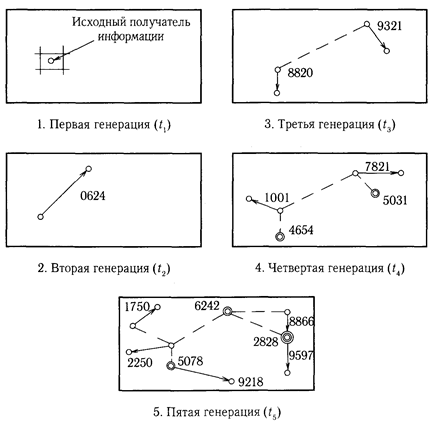
Рис. 20. Имитационное моделирование процесса диффузии. Начальные стадии модели иллюстрируются при помощи среднего поля информации. Цифры относятся к вероятности контактов, определяемых с помощью выборки случайных чисел. При внутренних контактах, т.е. контактах с ячейкой, на которую центрировано СПИ, в эту ячейку добавляется кружок
Для первой генерации из таблицы случайных чисел взято число 0624; поэтому сообщение передается к ячейке, лежащей к северо-востоку от исходного получателя информации, размещенного в очаговой ячейке. В целом рис. 20 показывает начальные стадии процесса диффузии. В каждой генерации СПИ по очереди центрируется над всеми очаговыми ячейками, располагающими информацией.
Поскольку в модели используется механизм случайной выборки, постольку при работе с ней мы получаем при каждом отдельном эксперименте иную картину географического размещения явления. Проведя на компьютере тысячи подобных экспериментов, мы обнаружили бы, что их суммарный эффект соответствует распределению вероятностей в первоначальном СПИ; следовательно, нам нужно вернуться к исходному распределению.
Модель Хагерстранда можно использовать при анализе не только простых процессов диффузии, исход которых заранее предсказан, но и при более сложных случаях, когда конечный результат диффузии нам неизвестен. Кроме того, модель поддается усложнению и модификации, так как служит логической основой для более реалистичных объяснений процесса диффузии. Кратко остановимся на основных направлениях этой модификации: 1) отказ от однородной поверхности; 2) оценка восприимчивости к диффузии и кривая насыщения; 3) границы и препятствия на пути процесса диффузии.
При замене однородной равнины иерархией населенных пунктов значения вероятностей должны быть отнесены не к ячейкам решетки, а к связям между населенными пунктами.
Для учета неравномерности заселения территории можно несколько изменить правило 1 и допустить, что население распределено нерегулярно и что в разных ячейках содержится неодинаковое количество людей. В этом случае вероятность контакта станет функцией не только расстояния между очагами-ячейками и ячейками, куда поступает информация, но и числа людей в каждой ячейке. Простым умножением мы получим взвешенное произведение вероятности контакта вместо исходного, полученного для равномерного распределения 1 человек — 1 ячейка; в формализованном виде мы получим простую формулу: Перейти на страницу: 34 35 36 37 38 39 40 41
Другое по географии
Геграфия рекреационных ресорсов Республики Дагестан
Дагестан, как и в целом, Кавказ, издавна привлекал внимание путешественников. Дагестан в переводе означает «страна гор». Это яркий и пестрый мир, полный поразительных контрастов, уникальных ландшафтов, редких животных и ...